Được học đại học trong ngành học yêu thích, tại ngôi trường yêu thích là ước mơ của mọi học sinh khi vừa bước qua 12 năm học phổ thông. Thế nhưng, cách thức tuyển sinh của Bộ Giáo dục trong 2 năm nay đã khiến nhiều bạn học sinh không thể thỏa ước nguyện ấy. Chưa nói về đề thi hay công tác chấm thi, cách mà Bộ buộc các trường thực hiện tuyển sinh đã khiến cho các trường khó tuyển học sinh chất lượng, còn thí sinh khó vào được trường, ngành mong muốn. Đơn cử, khối trường quân đội khu vực phía Bắc tuyển bổ sung sau đợt 1 gần 1.200 học sinh, trong khi có hàng chục học sinh đòi rút hồ sơ ra khỏi trường Đại học Bách khoa Hà Nội.
Vậy có cách nào khắc phục được tình trạng này không? Câu trả lời là có và lời giải cho vấn đề này đã được Giáo sư Ngô Bảo Châu và nhóm Đối thoại Giáo dục VED đưa ra vào nữa cuối năm 2015 (tuy nhiên không hiểu sao Bộ giáo dục đã phớt lờ phương án này). Lời giải này chính là áp dụng thuật toán DAA của Gale và Shapley.
Ngoài ra thuật toán còn dẫn đến những nghiên cứu, ứng dụng thú vị mà chúng ta sẽ tìm hiểu trong tầm hiểu biết của bậc THPT.
I – LỊCH SỬ
Hai người đầu tiên nghiên cứu về bài toán Hôn nhân bền vững (Stable Marriage Problem) là Lloyd Stowell Shapley (2/6/1923 – 12/3/2016) – nhà Toán học người Mỹ với nhiều cống hiến quan trọng trong lĩnh vực Lý thuyết trò chơi, giải Nobel Kinh tế 2012- và David Gale (13/12/1921 – 7/3/2008) – nhà Toán học, Kinh tế học người Mỹ, giáo sư danh dự tại University of California, Berkeley. Những năm 1960, Shapley và Gale quan sát thực tiễn và nhận thấy: rất nhiều hành vi của loài người liên quan đến việc ghép đôi, tạo mối quan hệ, ví dụ như đưa gặp gỡ kí kết hợp đồng giữa người mua và người bán hay tuyển sinh. Họ bắt đầu nghiên cứu của mình từ trường hợp đơn giản nhất: ghép đôi 1 – 1.
Từ trường hợp ghép đôi 1 – 1, họ tìm ra thuật toán DAA (Deferred Acceptance Algorithm-tạm dịch là “Thuật toán Chấp nhận trì hoãn”) và công bố vào năm 1962. Đến những năm 1980, Alvin Elliot Roth (18/12/1951) – nhà Kinh tế học người Mỹ, hiện đang giảng dạy tại Đại học Harvard – đã không ngừng nỗ lực tìm ra các giải pháp từ thuật toán này để giải quyết các vấn đề thực tiễn. “Có công mài sắc, có ngày nên kim”, hơn 40 năm sau, Giải thưởng Nobel Kinh tế đã được trao cho Roth và Shapley cho những cống hiến về “Lý thuyết phân phối ổn định và thực tiễn về tạo lập thị trường” (“the theory of stable allocations and the practice of market design”)
II – TÌM HIỂU BÀI TOÁN
1. MỘT SỐ KHÁI NIỆM
- Đồ thị
: là một tập hợp gồm V đỉnh và E cạnh (
). Ở đây ta chỉ xét đơn đồ thị vô hướng.
- Bipartite graph (đồ thị lưỡng phân hay đồ thị hai phía): là đồ thị mà tập các đỉnh có thể chia thành hai tập đỉnh sao cho các cạnh chỉ chạy giữa hai tập đỉnh này.
- Matching: trong đồ thị lưỡng phân
, một matching là một tập các cạnh thuộc E sao cho không có hai cạnh nào có chung đỉnh.
- Perfect Matching: Trong đồ thị lưỡng phân
với
sao cho mọi cạnh thuộc E đều chạy giữa A và B, ta nói A có một perfect matching với B khi tồn tại một matching mà mọi đỉnh thuộc A đều là một đỉnh của một cạnh trong matching đó.
2. BÀI TOÁN
Chúng ta hãy xét trường hợp kết đôi 1 – 1 mà các nhà Toán học hài hước gọi là bài toán hôn nhân (Marriage problem).
Bài toán 1: Có tồn tại hay không cách ghép cặp N cô gái với N chàng trai sao cho ai cũng lấy được người mình có cảm tình. Ở đây một người có thể có cảm tình với nhiều người khác giới.
Bài toán này được giải bởi nhà Toán học Philip Hall (11/4/1904 – 30/12/1982) vào năm 1935. Ông đã tìm ra điều kiện cần và đủ để tồn tại một cách ghép thỏa yêu cầu:
Hall’s marriage theorem (sau đây ta tạm gọi là định lý Hall): Consider a bipartite graph G = (V,E) with partition . For any set
, let N(S) denote the set of vertices (necessarily in B) which are adjacent to at least one vertex in S. Then, A has a perfect matching to B if and only if
for every
.
Chuyển về ngôn ngữ “tình cảm” và chỉ xét định lý trong trường hợp |A| =|B| = N: Ta nói rằng cô gái A được nối với chàng trai B nếu cả hai người có cảm tình với nhau. Như vậy một cô gái có thể được nối với nhiều người và ngược lại, một chàng trai có thể được nối với nhiều cô gái. Gọi N(X) là tập hợp những chàng trai mà ít nhất một cô gái thuộc tập X nối với anh ấy (X là tập con bất kì của tập N cô gái ban đầu). Khi đó, tồn tại cách ghép đôi sao cho ai cũng lấy được người mình có cảm tình khi và chỉ khi với mọi X là tập con của tập N cô gái.
Lời giải. Mệnh đề cần chứng minh hiển nhiên đúng cho trường hợp N = 1. Ta sẽ chứng minh quy nạp theo N mệnh đề này.
Giả sử mệnh đề đúng đến N = k. Xét N = k + 1. Gọi tập k + 1 cô gái là tập S, tập k + 1 chàng trai là S’. Dễ thấy chiều thuận của mệnh đề hiển nhiên đúng. Ta xét chiều nghịch của mệnh đề: giả sử với mọi X là tập con của tập S.
- Trường hợp 1: Tồn tại tập Y là tập con của S sao cho |N(Y)| = |Y| và 0 < |Y| < |S|. Xét tập con X bất kì của S/Y, ta có
. Thật vậy, giả sử
, khi đó
, mâu thuẫn với giả thiết quy nạp. Khi đó, theo giả thiết quy nạp, tồn tại cách ghép đôi thỏa mãn yêu cầu từ Y đến N(Y) và từ S/Y đến S’/N(Y). Vậy mệnh đề đúng với N = k+1 trong trường hợp này.
- Trường hợp 2: Không tồn tại tập con Y nào của S sao cho |N(Y)| = |Y| và 0 < |Y| < |S|. Khi đó, chọn một cô gái x bất kì, sau đó ghép đôi cô gái này với bất kì chàng trai y mà cô gái có cảm tình. Ta sẽ chứng minh với mọi tập con X của tập k cô gái còn lại, ta đều có |N(X)/{y}|
|X|. Thật vậy, giả sử tồn tại một tập con X của S\{x} sao cho |N(X)/{y}| < |X|. Nhưng ta có
theo giả thiết quy nạp nên
, mâu thuẫn!
Bài toán quy về trường hợp N = k. Vậy mệnh đề đúng với N = k + 1 trong trường hợp này.
Vậy mệnh đề đúng với N = k + 1 trong mọi trường hợp.Theo nguyên lý quy nạp, mệnh đề đúng với mọi N.
Đối với trường hợp |A| < |B|, cách chứng minh hoàn toàn tương tự.
Cách giải này cũng chỉ ra một lời giải cho bài toán thứ hai.
Bài toán 2. Hãy chỉ ra cách ghép cặp N cô gái với N chàng trai sao cho ai cũng lấy được người mình có cảm tình (nếu có).
Lời giải. Gọi tập hợp các cô gái là S, tập hợp các lời chàng trai là S’. Các quan hệ, kí hiệu sử dụng như lời giải bài toán 1.
Dựa vào cách chứng minh quy nạp của định lý Hall ở trên, ta có thuật toán:
- Đầu tiên, ta xác định N cô gái và N chàng trai có thỏa điều kiện của định lý Hall bằng cách duyệt từng tập con của S. Nếu không thỏa, hiển nhiên không tồn tại cách ghép, kết thúc. Nếu thỏa, ta thực hiện bước hai.
- Xác định có tồn tại tập con X của S sao cho
hay không. Nếu tồn tại, ta thực hiện thuật toán với các cặp tập hợp X và N(X), S\X và S’\N(X). Nếu không, ghép đôi một cô gái x bất kì với một chàng trai y bất kì mà cô ấy được nối. Ta thực hiện thuật toán với S\{x} và S’\{y}.
Nhược điểm của việc ghép đôi kiểu này là sự không ổn định nếu ta xét đến việc cô gái (chàng trai) có cảm tình với người này hơn người kia. Giả sử tồn tại cặp a – b và cặp x – y mà a thích y hơn b và y thích a hơn x, khi đó có khả năng dẫn đến hiện tượng ngoại tình, cách ghép đôi không còn hiệu quả. Ta xét đến thứ tự cảm tình của các cô gái và chàng trai.
Xét N cô gái và N chàng trai, ta giả sử rằng mỗi cô gái xếp thứ tự cảm tình với N chàng trai và mỗi chàng trai cũng có một thứ tự cảm tình với N cô gái. Các thứ tự này tăng nghiêm ngặt. Ta có bài toán sau:
Bài toán 3 (Stable Marriage Theorem). Một cách ghép cặp bền vững luôn luôn tồn tại, với mọi đồ thị lưỡng phân và mọi bộ sắp thứ tự ưa thích. (A stable matching always exists, for every bipartite graph and every collection of preference orderings).
Ở đây ta xét trường hợp |A| = |B| = N, trường hợp tổng quát tương tự: Luôn tồn tại một cách ghép đôi ổn định cho mọi N cô gái và N chàng trai với N là số tự nhiên bất kì
Ta có thể chứng minh mệnh đề này bằng cách chỉ ra thuật toán tìm cách ghép đôi và chứng minh thuật toán này luôn cho kết quả. Ta có bài toán:
Bài toán 4. Hãy chỉ ra cách ghép đôi N cô gái với N chàng trai sao cho không xuất hiện cặp nào ngoại tình.
Đã có nhiều người giải quyết bài toán này, trong đó cách giải của Gale và Shapley có ý nghĩa thực tiễn nhất, được gọi là thuật toán Gale – Shapley hay thuật toán DAA:
Thực hiện vòng lặp:
- Mọi chàng trai chưa đính hôn sẽ đồng thời cầu hôn người đang đứng đầu danh sách những cô gái mà họ chưa cầu hôn.
- Mỗi cô gái được cầu hôn sẽ so sánh những người cầu hôn và người mà cô đang đính hôn (nếu có) với nhau. Trong những người đó, ai có thứ hạng cao hơn trong danh sách của cô thì sẽ đính hôn với cô, còn những người còn lại bị từ chối và người đang đính hôn (nếu có) với cô bị hủy hôn.
- Mỗi chàng trai bị từ chối trong lần lặp này xóa tên cô gái từ chối họ trong danh sách. Mỗi chàng trai bị hủy hôn ước xóa tên cô gái đã hủy hôn ước trong danh sách.
Vòng lặp được thực hiện cho đến khi nào không còn chàng trai nào chưa đính hôn. Khi đó ta ghép đôi mỗi chàng trai với cô gái mà họ đính hôn. Kết thúc thuật toán.
Sau đây là một ảnh gif minh họa thuật toán.
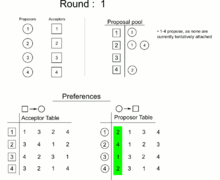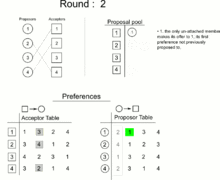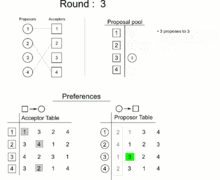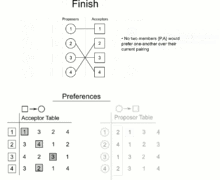
Bài toán 4.1. Chứng minh với thuật toán trên, mọi người đều được ghép đôi.
Lời giải. Dễ thấy rằng mọi người chỉ đính hôn với tối đa một người khác giới.
Ta xét một cô gái bất kì. Dễ thấy rằng sau khi được cầu hôn, vào mọi thời điểm kết thúc vòng lặp sau này, cô gái đó luôn được đính hôn. Ngoài ra, đối với một cô gái bất kì, do các chàng trai duyệt danh sách của họ từ trên xuống nên sau một số hữu hạn vòng lặp, cô gái đó sẽ được cầu hôn.
Bài toán 4.2. Chứng minh với cách ghép đôi nhận được từ thuật toán, không xuất hiện sự ngoại tình.
Lời giải. Theo thuật toán, đối với một cô gái bất kì, vào thời điểm bất kì, người đính hôn với cô có thứ hạng cao hơn những người đã bị cô từ chối và hủy hôn trong danh sách của cô.
Giả sử phản chứng: sau khi thực hiện thuật toán, tồn tại hai cặp cô gái – chàng trai là A – B và C – D mà D xếp hạng cao hơn B trong danh sách của A và A xếp hạng cao hơn C trong danh sách của D (A và D ngoại tình).
Do A xếp trước C trong danh sách của D nên khi thực hiện thuật toán, D cầu hôn A trước C. Sau đó D cầu hôn C chứng tỏ A đã từ chối hoặc hủy hôn với D. Khi kết thúc thuật toán, A kết hôn với B chứng tỏ B có thứ hạng cao hơn D trong danh sách của A, mâu thuẫn!
Vậy giả thiết phản chứng sai, mệnh đề được chứng minh.
3. TÍNH TỐI ƯU CỦA KẾT QUẢ
Thuật toán Gale – Shapley luôn mang lại kết quả với độ phức tạp . Ngoài ra, ta có thể định hướng được chiều hướng của kết quả sẽ có lợi cho bên nào. Ví dụ, ta hãy xét nhóm 3 cô gái A, B, C và nhóm 3 chàng trai X, Y, Z. Giả sử, thứ tự cảm tình của họ là:
A: XYZ ; B: YZX ; C: ZXY
và
X: BCA ; Y: CAB ; Z: ABC
Nếu ta chạy thuật toán với X, Y và Z “cầu hôn”, ta sẽ được kết quả là cách ghép cặp bền vững X-B, Y-C và Z-A. Cách này có lợi cho các chàng trai, các chàng sẽ được lấy người mình yêu nhất nhưng những cô gái sẽ phải lấy người xếp chót trong danh sách.
Nếu ta chạy thuật toán với A, B và C “cầu hôn”, ta sẽ được kết quả là cách ghép cặp bền vững A-X, B-Y và C-Z. Ngược lại với trường hợp bên trên, ở đây các cô gái được lợi nhiều nhất.
Ta được kết quả này có thể do những người “cầu hôn” duyệt danh sách của họ từ trên xuống, trong khi những người được cầu hôn chỉ được chọn người tốt nhất trong danh sách những người cầu hôn họ. Vậy bây giờ ta sẽ xem xét, chứng minh bên nào hưởng lợi nhiều nhất trong trường hợp các chàng trai cầu hôn các cô gái.
Bài toán 5. Xét tất cả các cách ghép đôi bền vững. Đối với mỗi chàng trai, gọi vùng khả thi là tập hợp tất cả các cô gái mà anh ta có thể cưới trong các cách ghép đôi bền vững. Định nghĩa tương tự với các cô gái. Chứng minh rằng trong cách ghép đôi là kết quả của thuật toán Gale – Shapley, các chàng trai luôn lấy được người có thứ hạng cao nhất trong vùng khả thi của họ, đồng thời mỗi cô gái lấy chàng trai có thứ hạng thấp nhất trong vùng khả thi của cô.
Lời giải.
- Đầu tiên ta chứng minh mệnh đề đầu. Giả sử phản chứng và xét M là chàng trai đầu tiên bị từ chối bởi cô gái đứng đầu vùng khả thi của anh ta (giả sử là W). M bị từ chối bởi W chứng tỏ ngay khi đó, W đính hôn với chàng M’ có thứ hạng cao hơn trong vùng khả thi của W. Do M là người đầu tiên bị từ chối bởi cô gái đứng đầu vùng khả thi nên W phải có thứ hạng cao hơn hoặc chính là W’ trong bảng xếp hạng của M’ (với W’ là cô gái đứng đầu vùng khả thi của M’). Bây giờ ta xét cách ghép đôi mà M kết hôn với W. Dễ thấy rằng W thích M’ hơn M, trong khi M’ cũng phải kết hôn với cô gái có thứ hạng thấp hơn W trong bảng xếp hạng của anh ta. Điều này dẫn tới sự ngoại tình, mâu thuẫn với tính bền vững! Vậy mệnh đề đầu đúng.
- Tiếp theo ta chứng minh mệnh đề hai. Giả sử phản chứng: trong cách ghép do thuật toán Gale – Shapley dẫn đến, tồn tại cô gái W nào đó kết hôn với M không phải là chàng trai xếp cuối vùng khả thi của cô ta. Theo mệnh đề đầu đã được chứng minh ở trên, W chính là cô gái đứng đầu vùng khả thi của M. Tương tự như trên, ta xét cách ghép đôi bền vững mà W kết hôn với M’ là chàng trai xếp cuối vùng khả thi của cô ta. Ta có: W thích M hơn M’, trong khi M phải kết hôn với cô gái xếp hạng thấp hơn W. Điều này dẫn đến W ngoại tình với M, mâu thuẫn với tính bền vững! Vậy mệnh đề hai là đúng.
Tuy nhiên, chúng ta xét tiếp một ví dụ khác. Có 5 ngôi trường A, B, C, D và E tổ chức tuyển sinh bổ sung thêm 1 học sinh theo điểm thi và 5 học sinh có điểm thi đôi một khác nhau. Giả sử các thí sinh này được xếp theo thứ tự điểm từ cao xuống thấp là I, II, III, IV và V.
Nếu ta chạy thuật toán với bên chọn là các trường: Lượt đầu các trường đều chọn I, khi đó I chọn trường I thích nhất và I “ghép đôi” với trường này, I bị xóa tên khỏi danh sách chọn lựa của các trường. Lượt tiếp theo các trường chưa chọn được học sinh sẽ chọn II,….
Nếu ta chạy thuật toán với bên chọn là các học sinh: Dĩ nhiên trong lượt đầu I “ghép đôi” với trường mà em thích nhất. Rồi đến II “ghép đôi” với trường mà em thích nhất nếu không trùng với trường của I hoặc “ghép đôi” với trường em thích thứ nhì. Tương tự như vậy đến hết.
Dễ dàng thấy rằng kết quả đưa ra trong hai kiểu chạy thuật toán đều như nhau và có lợi nhất cho các học sinh đạt điểm cao, lợi ích giảm dần theo điểm số.
Từ ví dụ trên ta thấy rằng, nếu một trong hai bên, hoặc trường hoặc học sinh, xếp hạng bên kia theo một tiêu chí thống nhất nào đó (ví dụ như điểm số) và không có hai đối tượng nào xếp hạng ngang nhau trong một bảng xếp hạng, thì chỉ cho ra một kết quả luôn có lợi cho bên còn lại bất chấp ta chạy thuật toán cho bên nào “cầu hôn”. Điều này dễ dàng chứng minh bằng phương pháp quy nạp, bạn đọc hãy thử chứng minh.
4. ÁP DỤNG THỰC TẾ
Thuật toán được sử dụng trong rất nhiều lĩnh vực, ví dụ:
- Y tế: phân phối nội tạng được hiến tặng đến các bệnh nhân để đảm bảo tương đối tính công bằng và mang lại lợi ích nhiều nhất có thể (trao đổi thận của thân nhân ở Hoa Kì).
- Công việc: Phân công các tân bác sĩ đến các bệnh viện (Chương trình quốc gia về phân bổ bác sĩ nội trú Hoa Kì NRMP đang áp dụng).
- Giáo dục: Phân bổ học sinh trung học tại New York và nhiều thành phố khác.
Bây giờ, chúng ta hãy thử áp dụng thuật toán vào việc tuyển sinh đại học:
Đầu tiên ta xét trường hợp đơn giản: Có m trường đại học, cao đẳng. Trường thứ i tuyển học sinh.Tổng cộng có
học sinh tham gia đợt tuyển sinh này. Giả sử mỗi trường sử dụng một tiêu chuẩn nào đó sao cho khi lập danh sách thứ tự học sinh theo tiêu chuẩn đó thì không có học sinh nào cùng một mức độ. Khi đó mỗi trường được một bảng xếp hạng các học sinh.
Trong trường hợp này, ta áp dụng thuật toán Gale – Shapley như sau:
Nếu tồn tại một học sinh chưa được xếp vào trường nào và danh sách của người đó khác rỗng thì: Xét trường đứng đầu danh sách của học sinh đó, nếu trường đó chưa có đủ học sinh theo chỉ tiêu, ta xếp học sinh đang xét vào trường này; ngược lại, nếu trường này đã đủ học sinh, ta so sánh hạng của học sinh đang xét trong bảng xếp hạng của trường với học sinh có các học sinh trong danh sách học sinh hiện tại của trường, nếu học sinh đang xét có thứ hạng cao hơn người xếp hạng cuối trong danh sách học sinh của trường thì ta loại học sinh đó ra, đưa học sinh đang xét vào. Cuối cùng ta xóa trường đó ra khỏi danh sách xếp hạng của học sinh đang xét.
Nếu không còn tồn tại học sinh nào có danh sách xếp hạng khác rỗng, ta kết thúc thuật toán, danh sách học sinh hiện tại của các trường trở thành danh sách chính thức.
Thuật toán này luôn đảm bảo những học sinh có điểm số cao vào được một trường nào đó, các học sinh top đầu vào được trường, ngành mình yêu thích và các ngành, trường tốt nhất chọn được học sinh giỏi. Nói cách khác, thuật toán đảm bảo được tính công bằng và cho các học sinh nhiều lợi ích nhất.
Trong thực tế, nếu tồn tại hai học sinh cùng hạng trong bảng xếp hạng của một trường nào đó, trường đó có thể xếp hạng học sinh này hơn học sinh kia theo thứ tự lựa chọn của hai học sinh đó.
III – CÁC BÀI TẬP
Đây là các bài tập người viết sưu tầm được có liên quan đến matching. Mời các bạn thử sức:
- Cho A là một ma trận vuông n x n có các phần tử là các số nguyên không âm và mỗi hàng, mỗi cột đều có tổng bằng số nguyên dương m. Chứng minh rằng: tồn tại m ma trận hoán vị
sao cho
. Ma trận hoán vị là ma trận có các phần tử là những số 0 và số 1, đồng thời mỗi hàng, mỗi cột đều chứa đúng một số 1.
- (Thổ Nhĩ Kỳ 1998/4) Có n người chuyển nhượng n căn nhà phân biệt. Mỗi người đánh giá, xếp hạng các ngôi nhà (không có hai ngôi nhà nào đồng hạng). Sau khi hợp đồng được kí kết, người ta có nhận xét là đối với tất cả các cách kí kết khác, tồn tại ít nhất một người phải nhận ngôi nhà mà người đó xếp hạng thấp hơn ngôi nhà được nhận trong bản hợp đồng đã cho. Chứng minh rằng: có ít nhất một người nhận được ngôi nhà anh ta/cô ta thích nhất.
- Cho S = {1, 2, …, kn}, và giả sử rằng
và
là hai nhóm tập hợp ứng với hai cách chia S thành n tập có số phần tử bằng k. Chứng minh rằng: tồn tại một tập T có số phần tử bằng n sao cho mọi phần giao
và
có lực lượng đúng bằng 1.
- Cho G là một đồ thị lưỡng phân có bậc của mỗi đỉnh đều bằng k. Chứng minh rằng G có một perfect matching.
- (J. Hirata.) Ta chia 52 quân bài tây của một bộ bài bình thường thành 13 nhóm, mỗi nhóm có 4 lá bài. Chứng minh rằng: ta có thể chọn ra từ mỗi nhóm 1 lá bài để được một nhóm lá bài có đủ hạng (ace, 2, …, king).
Hướng dẫn
- Ta có thể chứng minh bằng phương pháp quy nạp với n. Sử dụng định lý Hall, ta chứng minh được tồn tại n ô, mỗi hàng và mỗi cột có đúng một ô, sao cho các ô này chứa số nguyên dương. Tương ứng với n ô đó là một ma trận hoán vị cần tìm.
- Chứng minh bằng phương pháp phản chứng. Giả sử n người đó lần lượt là
. Rõ ràng theo giả thiết phản chứng,
không lấy được nhà mà anh thích nhất, giả sử đó là
mà phải lấy nhà
. Nhà
, giả sử được lấy bởi
, cũng không phải là ngôi nhà mà
…. Tương tự như vậy đến
và
với
sao cho
thích nhà
nhất. Khi đó, xét cách kí kết cho
lấy ngôi nhà
với
những người và nhà còn lại giữ nguyên như cách kí kết ban đầu, dễ thấy cách này không khiến cho ai phải nhận nhà mà họ xếp hạng kém hơn nhà họ nhận trong cách kí kết ban đầu, mâu thuẫn với giả thiết đề bài.
- Xét G là đồ thị lưỡng phân với hai phần là hai nhóm tập hợp A và B. Sử dụng định lí Hall, ta sẽ có điều phải chứng minh.
- Sử dụng định lí Hall.
- Sử dụng định lí Hall với một bên là 13 nhóm ban đầu, bên còn lại là 13 hạng (ace, 2, …, king), mỗi hạng 4 lá bài tương ứng 4 chất.
Tài liệu tham khảo:
- https://en.wikipedia.org/wiki/Lloyd_Shapley
- https://en.wikipedia.org/wiki/David_Gale
- https://en.wikipedia.org/wiki/Alvin_E._Roth
- https://en.wikipedia.org/wiki/Philip_Hall
- https://en.wikipedia.org/wiki/Hall%27s_marriage_theorem
- http://vnexpress.net/tin-tuc/giao-duc/tuyen-sinh/nhieu-thi-sinh-doi-rut-ho-so-trung-tuyen-de-nop-truong-quan-doi-3457701.html
- https://hocthenao.vn/2015/09/16/ve-viec-ap-dung-thuat-toan-daa-cua-gale-shapley-trong-xet-tuyen-doi-thoai-giao-duc/
- https://en.wikipedia.org/wiki/Stable_marriage_problem
- http://kinhdoanh.vnexpress.net/tin-tuc/quoc-te/nobel-kinh-te-2012-thuoc-ve-hai-nguoi-my-2723231.html
- Graph Theory, Po-Shen Loh, 24 June 2008
- Graph Theory II, Po-Shen Loh, June 2009



